Merge Sort
Like QuickSort, Merge Sort is a Divide and Conquer algorithm. It divides the input array into two halves, calls itself for the two halves, and then merges the two sorted halves. The merge() function is used for merging two halves. The merge(arr, l, m, r) is a key process that assumes that arr[l..m] and arr[m+1..r] are sorted and merges the two sorted sub-arrays into one. See the following C implementation for details.
1
2
3
4
5
6
7
8
9
10
MergeSort(arr[], l, r)
If r > l
1. Find the middle point to divide the array into two halves:
middle m = l+ (r-l)/2
2. Call mergeSort for first half:
Call mergeSort(arr, l, m)
3. Call mergeSort for second half:
Call mergeSort(arr, m+1, r)
4. Merge the two halves sorted in step 2 and 3:
Call merge(arr, l, m, r)
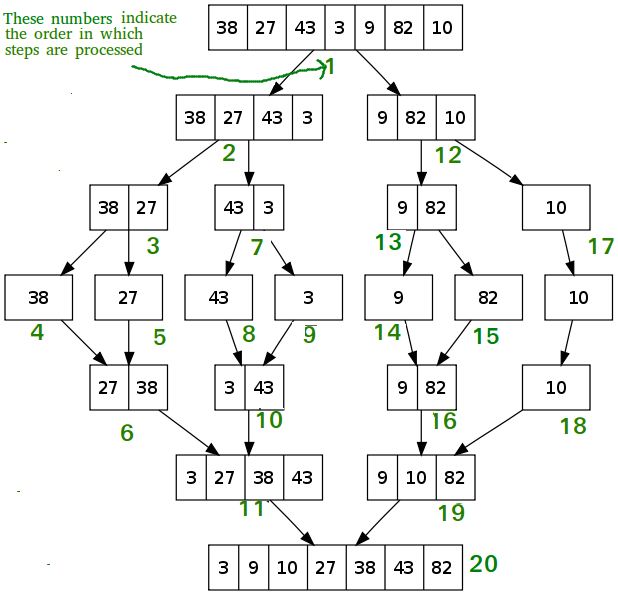
The following diagram from wikipedia shows the complete merge sort process for an example array {38, 27, 43, 3, 9, 82, 10}. If we take a closer look at the diagram, we can see that the array is recursively divided into two halves till the size becomes 1. Once the size becomes 1, the merge processes come into action and start merging arrays back till the complete array is merged.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
// C++ program for Merge Sort
#include <iostream>
using namespace std;
// Merges two subarrays of array[].
// First subarray is arr[begin..mid]
// Second subarray is arr[mid+1..end]
void merge(int array[], int const left, int const mid, int const right)
{
auto const subArrayOne = mid - left + 1;
auto const subArrayTwo = right - mid;
// Create temp arrays
auto *leftArray = new int[subArrayOne],
*rightArray = new int[subArrayTwo];
// Copy data to temp arrays leftArray[] and rightArray[]
for (auto i = 0; i < subArrayOne; i++)
leftArray[i] = array[left + i];
for (auto j = 0; j < subArrayTwo; j++)
rightArray[j] = array[mid + 1 + j];
auto indexOfSubArrayOne = 0, // Initial index of first sub-array
indexOfSubArrayTwo = 0; // Initial index of second sub-array
int indexOfMergedArray = left; // Initial index of merged array
// Merge the temp arrays back into array[left..right]
while (indexOfSubArrayOne < subArrayOne && indexOfSubArrayTwo < subArrayTwo) {
if (leftArray[indexOfSubArrayOne] <= rightArray[indexOfSubArrayTwo]) {
array[indexOfMergedArray] = leftArray[indexOfSubArrayOne];
indexOfSubArrayOne++;
}
else {
array[indexOfMergedArray] = rightArray[indexOfSubArrayTwo];
indexOfSubArrayTwo++;
}
indexOfMergedArray++;
}
// Copy the remaining elements of
// left[], if there are any
while (indexOfSubArrayOne < subArrayOne) {
array[indexOfMergedArray] = leftArray[indexOfSubArrayOne];
indexOfSubArrayOne++;
indexOfMergedArray++;
}
// Copy the remaining elements of
// right[], if there are any
while (indexOfSubArrayTwo < subArrayTwo) {
array[indexOfMergedArray] = rightArray[indexOfSubArrayTwo];
indexOfSubArrayTwo++;
indexOfMergedArray++;
}
}
// begin is for left index and end is
// right index of the sub-array
// of arr to be sorted */
void mergeSort(int array[], int const begin, int const end)
{
if (begin >= end)
return; // Returns recursively
auto mid = begin + (end - begin) / 2;
mergeSort(array, begin, mid);
mergeSort(array, mid + 1, end);
merge(array, begin, mid, end);
}
// UTILITY FUNCTIONS
// Function to print an array
void printArray(int A[], int size)
{
for (auto i = 0; i < size; i++)
cout << A[i] << " ";
}
// Driver code
int main()
{
int arr[] = { 12, 11, 13, 5, 6, 7 };
auto arr_size = sizeof(arr) / sizeof(arr[0]);
cout << "Given array is \n";
printArray(arr, arr_size);
mergeSort(arr, 0, arr_size - 1);
cout << "\nSorted array is \n";
printArray(arr, arr_size);
return 0;
}
// This code is contributed by Mayank Tyagi
// This code was revised by Joshua Estes
Output
1
2
3
4
Given array is
12 11 13 5 6 7
Sorted array is
5 6 7 11 12 13
Time Complexity: Sorting arrays on different machines. Merge Sort is a recursive algorithm and time complexity can be expressed as following recurrence relation.
T(n) = 2T(n/2) + θ(n)
The above recurrence can be solved either using the Recurrence Tree method or the Master method. It falls in case II of Master Method and the solution of the recurrence is θ(nLogn). Time complexity of Merge Sort is θ(nLogn) in all 3 cases (worst, average and best) as merge sort always divides the array into two halves and takes linear time to merge two halves.
Auxiliary Space: O(n)
Algorithmic Paradigm: Divide and Conquer
Sorting In Place: No in a typical implementation
Stable: Yes
Applications of Merge Sort**
-
Merge Sort is useful for sorting linked lists in O(nLogn) time. In the case of linked lists, the case is different mainly due to the difference in memory allocation of arrays and linked lists. Unlike arrays, linked list nodes may not be adjacent in memory. Unlike an array, in the linked list, we can insert items in the middle in O(1) extra space and O(1) time. Therefore, the merge operation of merge sort can be implemented without extra space for linked lists.
In arrays, we can do random access as elements are contiguous in memory. Let us say we have an integer (4-byte) array A and let the address of A[0] be x then to access A[i], we can directly access the memory at (x + i*4). Unlike arrays, we can not do random access in the linked list. Quick Sort requires a lot of this kind of access. In a linked list to access i’th index, we have to travel each and every node from the head to i’th node as we don’t have a continuous block of memory. Therefore, the overhead increases for quicksort. Merge sort accesses data sequentially and the need of random access is low. -
Used in External Sorting
Drawbacks of Merge Sort
-
Slower comparative to the other sort algorithms for smaller tasks.
-
Merge sort algorithm requires an additional memory space of 0(n) for the temporary array.
-
It goes through the whole process even if the array is sorted.