Fourier transform
소리에는 일정한 진동수가 있다.1
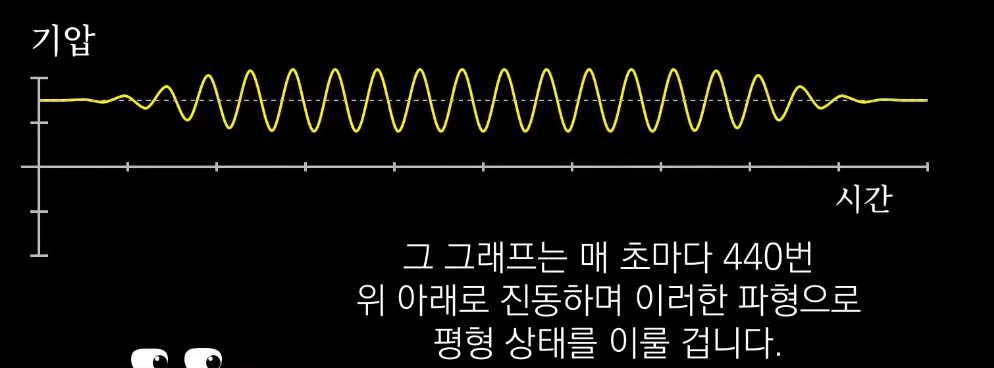
각 소리마다 일정한 파형이 존재한다.
두개의 소리가 동시에 들리면 어떻해될까?

두 소리의 합성으로 특정부분에서 파형이
증폭 될것이고,
상쇄될것이다.
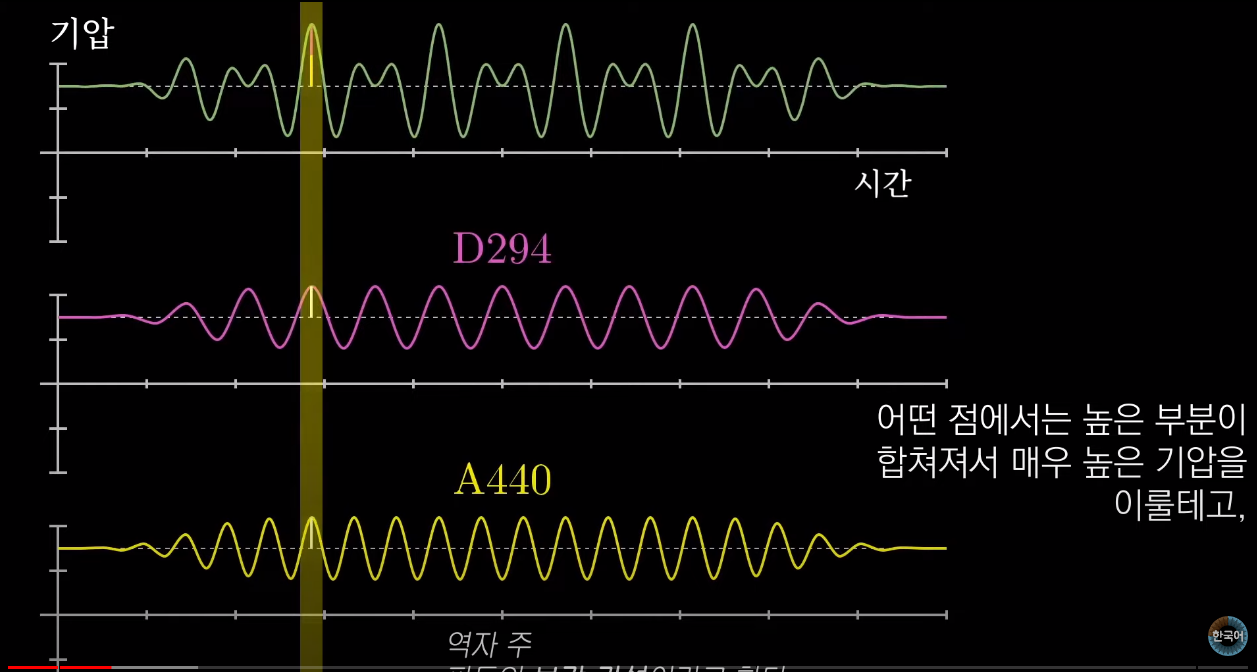
증폭을이루고(보강간섭)

상쇄된다(상쇄간섭)
푸리에변환의핵심
이런 모양의 신호를 받았을때
각 성분을 따로 분리할수있을까?

방법
1초에 3번 진동하는 신호의 그래프

이 그래프를 한원에 감아보면
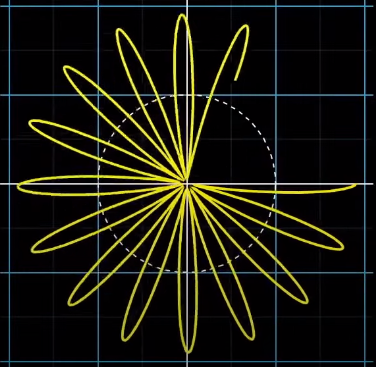
여기서 각 노란색 점은
시간에따라서 원주위를 회전한다.
이떄 노란색점의 좌표는 1초에 3번진동하는 그래프의 파형의 높이와같다.
파형이 높으면 원점에서 멀어지고
파형이 낮으면원점에서 가까워진다.
원이 한바퀴 도는데 2초가 걸리도록 그림을 그려보면

이떄 백터값(노란색점 좌표값) 은 1초에 원의 반바퀴를 돌고있다.
이떄 중요한건
2가지 신호가 존재한다는것
신호자체의 진동수가있고(1초에 3파형)
우리가 설정할수있는 백터의 진동수값이 있다는 것이다.(1초에 반바퀴)


이때 신호의 진동수 (기존파형)와 감는진동수(우리가 설정하는 값)
을 일치시키는 경우(1초에 3번)
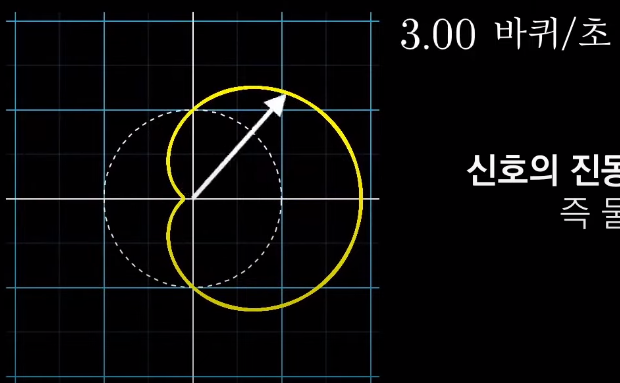
파형이 높은곳은 오른쪽으로몰리고
낮은곳은 왼쪾으로 몰린다.
무게중심을생각해보면
설정한 진동수에따라
중심좌표가 원을 중심으로 반복된다.



무게중심이 예외적으로 치우치게 되는경우
진동수를 일치시킨경우


두 파형의 합성

이 그래프의 무게중심 좌표를 구해보면

2와 3의 진동수에만 치우친 값을 가진다.
따라서
원의 중심 좌표를 구하는 공식을 알 수있다면
합성파형의 각 성분을 분리할 수있다.
원의중심구하기 == 푸리에 변환
공식
오일러 공식으로 원둘레 좌표를 구할 수 있음
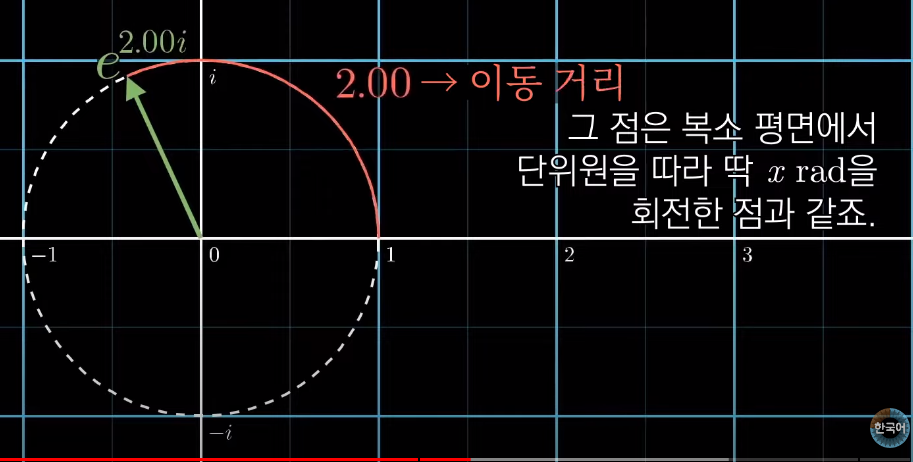
이를 이용해 1초에 단위원 한바퀴 도는걸 표현하면


지수에 진동수를 곱해보면


10초에 한바퀴 돌게됨.
왜?
시간이 10초증가해야 1이되기떄문에
1/10 * 10 = 1
관습적으로 푸리에 변환은 시계방향의 회전을 다루기떄문에
지수에 마이너스를 곱


1초에 3번진동하는 파형의 사인그래프 함수


원을 감는 파형의 공식
무게중심구하기
각좌표점의 평균을구해보면

점의 개수가 늘어날수록 근사치가 정확해짐
무한대로 확장하면

헌데 실제 푸리에함수는 시간으로 나누지 않는다

실제 무게중심을 구하는것이 아니라
무게중심에곱해진 값을 보는것이기떄문
그래프를 3초간 측정했다면
무게중심 곱하기 3한값을 측정하는것
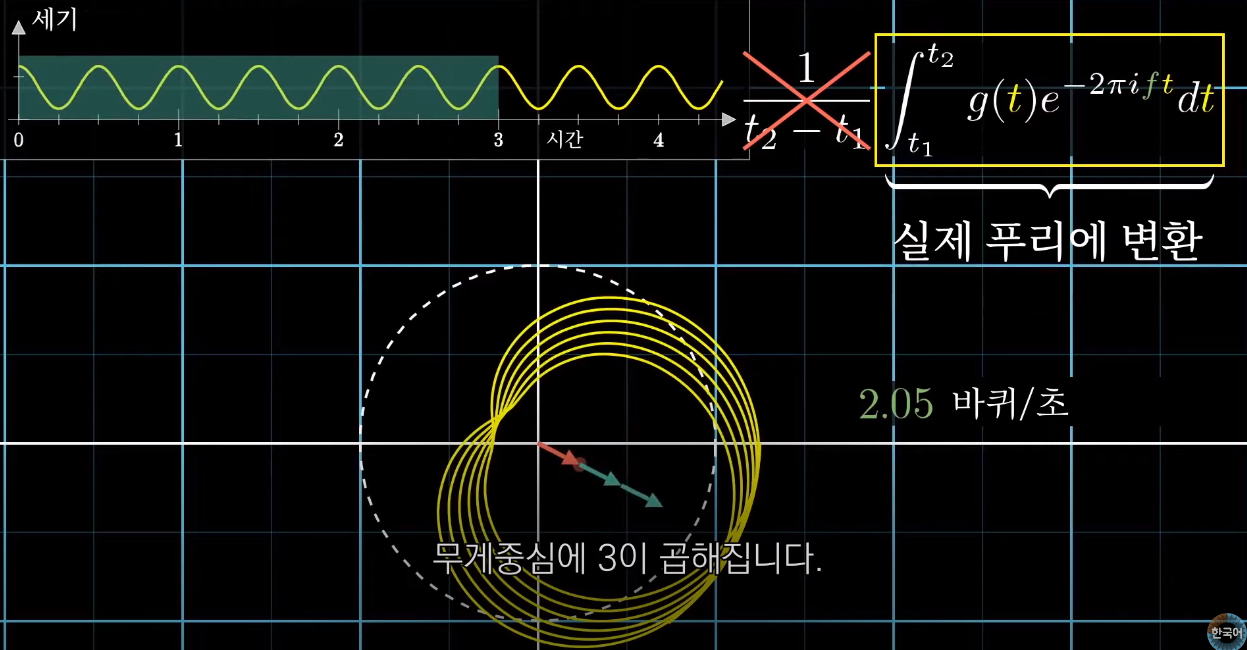
측정시간이 길어지면 푸리에값도 무한히 증가함

헌데 합성파형에서 두 진동수가 조금만달라도
중심의 좌표 크기가 상쇄됨.
